½ 問題 (1)
●力学とのアナロジーを作ろうとすると、エネルギーのところがなかなか難しい。初歩の力学における「仕事」は摩擦のない系における運動エネルギーの蓄積の話が混ざっているように思える(練習問題では出てきた)。電気回路学と対応づけを明確にしようとするとここは丁寧に。
まずは「摩擦に逆らってものを動かす」ことに焦点を当てて語り、
その後、運動エネルギーの話とともに、力を加えて速度が変わる話などを加えていくのがよいか。
最初から「“質量m”の物体」とするとmisleadingになる。最初は「摩擦に逆らって動かされる物体」である。ダンパーみたいな構造のものでもよいかもしれない。「摩擦器」とでも言おう。
・力を加える → 移動して力を加えるのをやめたらすぐ止まる (散逸系)
移動して力を加えるのをやめたらそのときの速度を維持 (保存系)
変形する (保存系)
「こんにゃく」のような、ある程度男性変形する物体を持ってきて、
・速く、ちょん、と押すと 変形 → k
・ゆっくり押すと摩擦に逆らって移動 → Γ
・押すのをやめてもヌルヌルのせいであと少し移動 → m
と説明できる。(全部分かった人なら伝わるが初心者は「ポカン」とするだけかも)
この違いは、一回学んだ人には語ることができるが、「保存系」「散逸系」すら知らない初心者にはなかなか難しいだろう
機械系の話
・Fが動摩擦力(一定)の場合も1/2 はかからない
・Fが速度に比例するダンピング力の場合はどうか (機械ー電気アナロジーにおいて抵抗に対応するので、多分1/2はかからない)
½ 問題 (2)
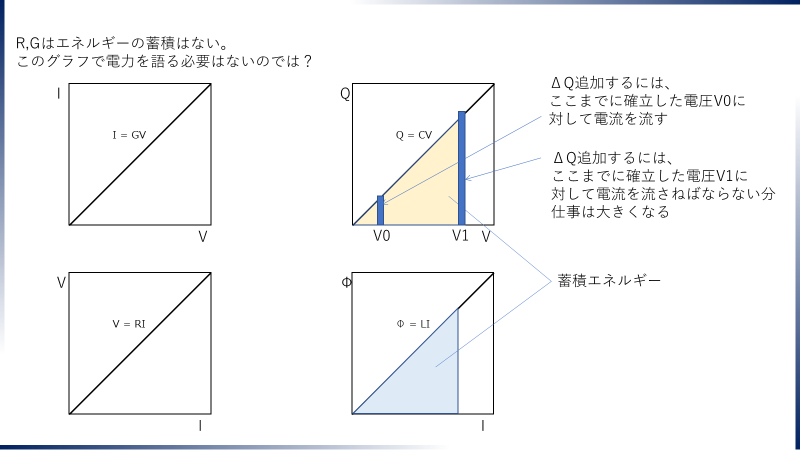
・D=εE、B=μH これらもばねと同じく、1/2 の係数がかかる。
・抵抗に流れる電圧と電流には1/2の係数がかからない。
・これは、散逸を表している。多数の粒子の加速~衝突 がランダムに起こると、蓄積された運動エネルギーを回収できなくなる。
・抵抗によるエネルギー消費は散逸現象そのものといえるか。
「多数の荷電粒子による現象」としてオームの法則があり、それをシンボリックに担う素子として抵抗が考えられた、といえるか?
「多数の荷電粒子による現象」としては、他には、電池などにみられる化学反応があるだろう。(おそらく、化学反応は反応式に書かれただけの分子だけで済むものではないはず)
電子は、電界により加速されるが、平均してτ後に結晶イオンに衝突してエネルギーを失う。平均すると、電流が一定の力を受けているように。
抵抗のある系は時間反転に対して不変ではない(ハミルトン系ではない)
Maxwell方程式系から、直接、RIと ½ΦI ½QVを導くことができそうである。
電流に対する電力の求まり方は、電流密度や導電率の積分でダイレクトに出せるが、電界、磁界は、∫EdDなど、時間を陽に含まない表現になる(これ、ハミルトン系だからだろう)
Poyntingの定理:電磁場に蓄えられるエネルギーの時間微分=Joule熱+放射エネルギー
とあり、RIと、1/2 LI^2, ½ CV^2は別物
これを最初に話すのもありか。電磁気学の全体像が分かるように思える。
オームの法則と電荷保存の式から、あらゆる電荷分布が減衰、つまり散逸系であることが言えてしまう。 (砂川、P77)
だとしたら、電磁気も含めて、What is Resistor?から始めるとよい。
●松澤 新しい電気回路
・第3章 容量~デジタル回路の電力消費の筋が明確にできていない。知っていること並べただけじゃないか。脈絡が甘い。
P43で容量は電力を消費しない、と言ってるが、そのあとに、エネルギー保存の話とか、SWでぱちぱちやると電力が消費されるとか、いろいろ出てくる。
書いてあることを総括すると、「非断熱的電荷移動においてエネルギーが散逸する」なんだが、そこまで言い切ってない。
電源の概念の提示の場所が悩ましい
断熱充電は摩擦によるロスなしでばねを変形させようというものでないか? (あまり現実的ではないし、ゆっくり充電する方法の極限でもないように思える。要は摩擦を無視しているわけだから)
実際にRamp入力で解いてみようか・・
・3.1.4 容量のエネルギー保存の件
まだ回路の応答を提示していないので、妙な解き方をしているが、これは結局微分方程式を離散化しているだけじゃないですか?
エネルギーに対する洞察を最初に持ってくるとハマる。案の常、Lagrange方程式にまで言及しているが、応答を教えた後(そうしかできない)
こんなことせずに、先に応答を教えましょう。エネルギーはどうせ保存しないんだから。
「保存量」という高尚な概念は、まずは示唆にとどめて、「電荷保存」「鎖交磁束保存」という地べたの保存則と応答解析をしっかり身に着けてもらう。
保存系と散逸系
最初に、保存系と散逸系の違いを説明。時間反転の話も上手く入れられると良い。
脱線ネタとしては、ケプラー運動に対応させる電気回路が示せると面白い。楕円軌道に対応させられる回路は存在するだろうか。
運動の方向と力の向きが直交しているとエネルギー増減はない。円運動が該当する。楕円運動は直交しないが、一旦失ったエネルギーは後に回収されるため、運動の永続性は失われない。
保存系は現象の基本的な枠組みを与える。適切な物理量を選択して共役な変数にアサインすることで、解析力学のツールが使える。なお解析力学は裏方理論なので、新理論を構築する時以外は知らなくても心配は不要である。
ただ、もし世の中保存系だけならば、我々は、美しい時間反転対称性と、永久に運動し続ける様をを鑑賞することしかできないだろう。
散逸系は物理の立場からは異物かもしれないが、エネルギーの生産や利用に着目する工学では主役である。その中では保存系に主に寄与する要素は「寄生素子」などと呼ばれて嫌われる対象になる。