● 抵抗とは
〇こだわり:物理的側面は全てオームの法則のバリエーションで語りたい
・抵抗 の概念を天下り的に与えて回路網を解かせたり、定理群を説明するのではなく、抵抗ってどんなの?という話から入って、深掘りする過程で、エネルギー、散逸、仕事、回路定理群、非線形性、寄生素子、分布定数、そしてイデア部分の定義をしてみたい。
・企業新人向けならば、「抵抗とはなにだったか」と問うて、まずV=RI がホントか?と問い続けて深掘りすることも可能ではあるが、もうひと越えできると読者は増えるだろう!
20万ボルトの高圧電流って何よ!からでも良いか
・抵抗の話を電源とインピーダンスの文脈に乗せても良いかもしれないが、積極的に設計に行く抵抗と、寄生的なものの対比に工夫が必要
電球などの具体例を示した上で、抵抗の周辺をいろいろ考え、その理解のために電磁気学を援用し、さらに電磁気学をベースにした伝送線路へと導くように、話を作る。
順番としては従来通りだが、抵抗の段階で徹底的に深掘りする。
(1)熱を出すもの、白熱電球、ヒーター
(2)光らない抵抗、抵抗器:電子デバイスを最適なバイアスで動作させるために大活躍
(3)抵抗とみなせる現象(エネルギー変換、伝送・・伝送線路も含んでいる)
なぜ光るのか、そもそもなぜ抵抗が発生するのか、線形とは、非線形、温度係数、寄生C、L、時間遅れ+金属電子論、伝熱、黒体放射(量子力学)、光半導体)ことで、理論としての広がりを最初から準備するところが特徴
熱抵抗、磁気抵抗などの概念も紹介したい
###
図書調査 ・・・ 「抵抗」概念の導入
★電気学会大学講座
・「加えられたエネルギーを蓄積することなく消費する素子」
・何のためにそんなものがいるのか? の説明がない。天下り過ぎる。
★なっとくする電気回路(國枝) 重層的に解説
1
電源が出すエネルギーを消費して熱エネルギーに変える
例 電熱器 暖房や調理に利用
電気回路中では電圧や電流の大きさの調整 (電子デバイスにはバイアスが必要。段間の電位合わせも必要。この組み合わせを上手に作るのが回路設計)
代償としてやむを得ず電力消費
2
銅、ニッケル電圧を加えると電子が移動して電流が流れる
電圧と電流は比例している オームの法則
抵抗率
短絡、ショート
開放、オープン
3
電力 単位時間あたりに電荷を移動させるための仕事
その前に
電位差 単位電荷を移動させるのに必要なエネルギー
電流 どれだけの電荷がどれだけの速度で移動したか
力学では、内積(力ベクトル、変位ベクトル)=仕事
閉路方程式は「電流はループだ」を墨守していた!
★エース電気回路理論入門(奥村)
電流の流れを妨げる素子を抵抗
#結構乱暴に聞こえる。保護素子でないならば定義にネガティブな言葉を使いたく無い #「供給電力最大の最適な抵抗値」が必要なシーンは特定すべきであろう
★電気学会大学講座
・「加えられたエネルギーを蓄積することなく消費する素子」
・何のためにそんなものがいるのか? の説明がない。天下り過ぎる。
★なっとくする電気回路(國枝) 重層的に解説
1
電源が出すエネルギーを消費して熱エネルギーに変える
例 電熱器 暖房や調理に利用
電気回路中では電圧や電流の大きさの調整 (電子デバイスにはバイアスが必要。段間の電位合わせも必要。この組み合わせを上手に作るのが回路設計)
代償としてやむを得ず電力消費
2
銅、ニッケル電圧を加えると電子が移動して電流が流れる
電圧と電流は比例している オームの法則
抵抗率
短絡、ショート
開放、オープン
3
電力 単位時間あたりに電荷を移動させるための仕事
その前に
電位差 単位電荷を移動させるのに必要なエネルギー
電流 どれだけの電荷がどれだけの速度で移動したか
力学では、内積(力ベクトル、変位ベクトル)=仕事
閉路方程式は「電流はループだ」を墨守していた!
★エース電気回路理論入門(奥村)
電流の流れを妨げる素子を抵抗
#結構乱暴に聞こえる。保護素子でないならば定義にネガティブな言葉を使いたく無い #「供給電力最大の最適な抵抗値」が必要なシーンは特定すべきであろう
電磁気・物質から語る電気回路論
★固体とはどんなものか
・固体は、原子核と電子で構成
・原子核と大部分の電子はまとめて+の電荷、これは動けない。
・いくばくかの電子が動いて、隣接する原子(イオン)や、同類の電子と相互作用
・全体として電気的に中性
・(A)もしーが過剰なら負に帯電、ーが不足なら正に帯電 → キャパシタ
・(B)ーが移動すると「電流」 →インダクタ
・ーが飛び出したらβ線、陰極線となり、固体の話ではなくなる。
・+、ーも存在し、再結合せずにそれぞれ移動できる場合プラズマといい、もっと難しい話が出てくる
★電流を流すものとしては、配線、電子デバイス、エネルギー変換要素があり、これらを組み合わせてエレクトロニクス
・もっと広く言うと、「オームの法則に従うものと従わないものの両方をうまく組み合わせて回路を作る」「その上位階層でエネルギー変換・伝送」~エレクトロニクス
・導体=電気配線とその仲間。オームの法則の話をする。
・電子部品=トランジスタなどの増幅動作やスイッチング動作を期待する電子デバイスに加え、オームの法則が成り立つとされる抵抗、L、Cがある。R、L、Cは設計されるものもあれば寄生でできてしまうものもある。それらにまとめて対峙できるような理論体系が電気回路論
・導線は、出入り口の定義さえしっかりやれば、「線電荷」と同一視できるはず。
・特殊相対論への自然な組み込みを射程に入れて、電流を「多数点電荷の移動」ではなく「線電荷」の縦方向への移動ととらえたらどうか。
電磁気学は点電荷から始めるが回路は線電荷から始めるのだ、と。
★固体中の電流は4態
・電子がぶつかりながら動く (固体で導体。電界で加速された運動エネルギーが結晶格子にすぐぶつかり散逸し熱に代わる)
・拡散電流 (電界がなくても濃度差で移動)
・超伝導電流 (クーパー対、抵抗0)
・エネルギー変換 (電流が電磁気法則に基づきエネルギー変換媒体として活躍する。等価回路でなんとか書ける)
★気体の電流は2態
・自由空間で電子が飛行する (陰極線、β線、時間とともに電界が仕事をして運動エネルギーとして蓄積)
・プラズマ電流 (正負の粒子がともに電流を担う)
★ Q 電流を積分すると電荷量の変化になることはわかりやすいが、電圧を積分すると磁束の変化になることはどのようにイメージするとよいか?
要するに電磁誘導を逆から説明しようとしているわけだが。 (Ampereの法則から遅れてFaradayの法則が発見されたぐらいだから、そもそもわかりにくいのだろうけど)
★抵抗の説明
電球、モーターなどの機器に電流を流して電気エネルギーを供給することで熱エネルギー(そして光エネルギー)や磁気エネルギー(そして運動エネルギー)を発生させることができる。電気機器に限らず、例えば単なる電線や基板上の配線パターンにおいても電球などと同様、電流を流すことで多かれ少なかれ発熱がある。
タコ足配線するとコンセントが熱くなるのを経験したことがあるだろう。もっとも、これは電気機器とは異なり、望まぬ結果ではある。
一般に、モノに電流を流すには、流す電流の大きさと、そのモノ固有の性質で決まる電圧を印加する必要がある。逆にいうと、ある電流が流れているということは、相応の電圧差が発生しているのである。電流を流そうとする外部からの力と電流に抗おうとする内部の力が平衡していると考えると、力学で言う作用反作用の法則に対応する。電気工学では、この性質のことを「抵抗」と呼ぶ。理想的には、電圧と電流は比例し、
V=RI
と書ける。回路においては比例定数Rが抵抗素子そのものであるかにように用いられることに注意されたい。
比例しない場合は、まずVがIの関数であることを示し、所与のIまたはVにおける微分係数を、小信号における等価抵抗と考える作法が実用的である。すなわち
V=f(I)
R=dV/dI=f’(l)
などとする。放熱の悪い状態で使用される抵抗素子は電流を大きくすると発熱で抵抗値が大きくなるため(小さくなるものも作ることは可能)、厳密にはVとIは比例せず、抵抗値も電流により異なる。
極端な例では、過去に高周波発振回路などに重用されたエサキダイオードがある。このRが負になるように動作電圧が設定される。このような素子は負性抵抗素子と総称される。
★電子回路設計への活用
電位差を与えるか電流を流すかのどちらによって内部に電位勾配を作る作用がある
任意の場所に電極を取り付けて所望の電位を取り出すことができる。
これをバイアスに活用している
★電流制限
電圧の喧嘩、例えば、充電器を考えてみるとよい
電圧の喧嘩はなぜまずいか先に言える
★抵抗を嘗め尽くす(本質編)
・そもそもどんな形をしているか(LSI、個別部品)
・オームの法則はイデアの話
・オームの法則に加えて電力P=VIの話も必要。
・そもそもなぜVIが電力なのか?または∫VIがエネルギーなのか?
・V=Edと、電界と距離に分けると、力x距離に帰着できるはず
・まず、電球、電熱器 ⇒ 光、熱エネルギー (光はやがては熱に)
・モーター、電気分解 ⇒ 機械エネルギー、化学エネルギー
・余談:
機械エネルギーは、移動→摩擦で熱エネルギー、
高いところに移動→重力エネルギー→いつか低いところに移動し熱エネルギー
変形・加工→温度上昇、さめる過程で熱エネルギー、捨てる時に焼却・スクラップ→熱エネルギー
・その場でエネルギーが変換されていると抵抗に”見える“
電気回路の例としては、トランス誘導モーターが使える
・保護素子としての動作は、エネルギー変換機能に含む
・2 つの機能 エネルギー変換、電子回路の動作点設計
・2つの作用 仕事する、散逸する
・2つの避けられない物理 電源の内部抵抗、配線抵抗
・要検討 以下、式解き含めて理論立てておくこと
・無負荷のチャージポンプやDC-DCコンバータを入力から見たとき、どんな等価回路か? ・そこに負荷をつけたらどうか
★「抵抗とはエネルギー変換である」と言い切れるか?
コイルとコンデンサは空間にエネルギーを蓄えている。一方抵抗のエネルギー消費は結晶の中の話。この違いは大きい。
また、放射抵抗(377Ω)は、同じ“抵抗”とはいえ、伝送線路のインピーダンスであり、終端されない限りエネルギー消費はせず、移動するのみ。
トランスで2次側負荷の有無によって、1次側からの入力インピーダンスはどう見えるか?
・後段のどこかで消費(散逸)が起こっていたら抵抗に見えるはず。この場合この等価抵抗がエネルギー変換をしているといえる。
#エネルギーは、「蓄積」「移動」「消費」のどれか
電気機器学のテキストを見るだけでも、結構複雑で、ちょっと無茶のようだが、散逸エネルギーも含めれば合っているはず。エネルギーフロー図なるものがあるわけだから。
入力から見ると、有効電力が回路に供給されているわけだから、その電力は、散逸も含めて変換されるか、どんどん蓄積されるかのどちらかである。
蓄積されない状況に限定すれば、抵抗でエネルギー変換されたといえる。
蓄積される状況ではどうか?
IでCを充電する場合・・これはCに見える。Rではない。しかし、これもエネルギー変換といえなくもない(運動エネルギーをポテンシャルエネルギーに変換している)
「電気エネルギー」より細かいことを言わなければよいか。(光だって、電界と磁界があって、分けて語ったりしない)
誘導モーターではOK 「電気機器学基礎論(多田隈、石川、常広)」 P.21
r2/s = r2 + (1-s)/s r2 第2項は機械出力を表す
電気ー機械変換においては、「誘導起電力の発生と電磁力の発生が同時に行われて「仕事」をしている 「電気機器学基礎論(多田隈、石川、常広)」 P.6
P=ei が Pm=vF=τω と同じことだ、と言っている。
アンテナも該当する 放射される電力は放射抵抗での消費電力であらわされる。
純リアクタンスでは ∫ei dt が0になる。これが0でない部分が抵抗成分(エネルギー変換)成分であるはず。
ei の偶関数部と奇関数部 (正確ではない)のようなとらえ方をすることで、正弦波定常状態からの脱却ができるのではないか? (山村理論なのかもしれない)
何と、Jouleがそう言ったらしい(百万人の電気技術史)
★抵抗に見えるもの
Q 電池は巨大なキャパシタか?
これを充電するときに、電圧を印加して電流が流れている。あるいは電流を印加して電圧が発生。これは抵抗に見えるといえなくもない。
化学変化を伴っているはずなので、単に巨大なCを充電していると思わないほうがよいだろう。エネルギー変換といえる。
フォトダイオードは非線形抵抗としてよい。VI → 光 + ジュール熱
Q 光電変換は、hνが電子の数に変換される。それが蓄積されるところはCであるが、変換されるところそのものは抵抗で書いてよい?
あるバイアスに対して、光量に応じた電流が流れる。これは光変調抵抗としてよいのか光変調電流源とすべきなのか?
Rをエネルギー供給源に使ってよいのか?
少なくとも散逸系ではありえない。発電機などは?誘導発電機はsが負になり、負性抵抗がエネルギー供給
センサも負性抵抗モデルで書けばよい?
PDは、正バイアスにおいて、光が当たると電位が下がる、つまり電流が流れ出ていることになるので、これは負性抵抗といえる。
熱電対、サーミスタはそもそも抵抗である。
Q マイクは?
ダイナミックマイクは、発電機と似ているだろうが、コンデンサマイクの等価回路は容量で書かれている。さあ、どうする?
容量が変調された分を取り出すならば、抵抗に見えないかな?
Q=CV でCが変調されたらどうなるか?
I=dQ/dt=dC/dt *V ・・dC/dtが1/Rだ!
大学課程電気回路(1)P202に、電気ー機械系のモデルが書いてあった(静電系、電磁系共。それらは双対のようである)。非線形項は陽には記述されず、ジャイレータっぽい表現
Q 電界を印加すると電流が流れるというのはイメージしやすいが、逆の、電流を流すと電位勾配が発生することを、抵抗の概念抜きで語ることができるだろうか?
電界印加の場合 電流が流れたがるが、無限に流れるわけにはいかず、摩擦で上どまる (滝が落ちるイメージ)
電流を流す場合 電流連続を維持するためには妨げる効果がある箇所には電界が発生する (むしろ滝登りのイメージかもしれない)
#どちらも電子から見ると滝登りだ
★抵抗の使いこなし知識
・電子回路での活用
・抵抗器は電位勾配を利用可能か物理現象化する。我々は、抵抗器の組み合わせ、または、タップを付加して取り出したりして好きな電位を作ることができるのである。
・抵抗の仕組みを説明するときには端折られがちなこのニッチな性質こそ、電子回路技術を成り立たせているのである。
・抵抗は電位差を与えるか電流を流すかのどちらかによって、内部に電位勾配を作る作用がある。これをバイアスに活用している。
・能動素子を組み合わせると電圧を与えて電流を取り出すこともできる(電流源)
・電源から見れば負荷回路は抵抗に見える
・現実の難しさ(面白さ)
・ノイズ (熱雑音がある。勉強すれば設計には使えるようになる。ただ突き詰めると一定の「理論限界」が見えてくるかもしれない。それをどのような手段で克服するかが競争力の源泉となる。その限界は「真の限界」ではないことも多い)
・発熱して抵抗値が変わる。発火点以上に温度が上がると焼損
・発熱してほかの回路素子に熱が伝わり特性変動
・精度(数%~20%)
・選別が必要になる場合もあるが、20%でも設計可能な回路も多々あるので臨機応変に対応する
・集積回路ではマッチングを期待した設計が可能でそれを支えるためのパラメータも用意されている(のが普通。用意されていなければ要求してよい)
・配線にも電気定数があり、抵抗成分も存在する。配線のCと相まって、伝搬遅延(Elmore Delay)に。
・オームの法則の拡張
・V=RI → V=(R+ΔR)(I⁺ΔI)≒RI+RΔI+ΔRI
まず、全微分で書くことができる
dV=∂V/ ∂I x dI + ∂V/ ∂R x dR = r dI + SVR dR
r: 小信号抵抗 SVR:素子感度
TCFは直接Rの温度依存性とかけるが、これはあくまで特定の回路モデルにおいて採取したパラメータであることに留意。場合によってはGの温度依存性としたほうが扱いやすかったりする。
●抵抗にこだわる 1
<抵抗とは>
・オームの法則は実験的に導かれたもの、ということ
・後付けで現象論的説明(衝突までの時間の2乗平均の問題を明確にしたい)→ 固体電子論 (ドルーデモデル。脱線:誘電体モデル、半導体、磁性体)
・実験の前提が変われば、その通りにはいかないよ、と。それを追究して体系を作っていくことができる。
もちろん隣接領域からの手助けも(オームの法則を確認するには電気化学の成果である電池が必要だが、その電池はオームの法則を満たさない)
・なぜ重宝するのか
・エネルギー変換を表す等価回路素子。電球、ヒーター。特性Z(同相の電流と電圧の比、同相の電界と磁界の比)力学的な「仕事」に起因する電気現象も表現(発電機、電動機)
・同相、すなわち単純に比例している成分がエネルギー変換を表しているのがわかりやすい。単純な計算で変換されたエネルギー(電力)が求められる。
・動いていても、力がかかっていて仕事していない例:重力による円運動(力と動きが直交)、楕円運動(一周回るとチャラになる・・L、C回路の比喩に使えないだろうか)
・まずエネルギーを伝えたいところに等価素子として抵抗を置き、つづいてその「うまくいかなさ加減」を様々な素子で表現していくことができる。
・さまざまな電気電子デバイスの非理想性を表現する等価回路素子。電池の内部抵抗、配線抵抗、これもエネルギー変換(散逸)の一つ。
・応用1:信号の大きさ(振幅、電力)を調整
・応用2:応答パフォーマンスの調整、最適化(ダンピング、整合) ケツ拭き係
・応用3:必要な直流電位を作成(タップ取り出し、分圧)。能動素子に適正な動作電位を与えるのに必須。これがないと動作電位の数だけ電源が必要になる。その代償として電力消費
<等価回路素子としての抵抗>
・スイッチ On抵抗 理想的には電力0
・電池の内部抵抗 @1ポート → 電源の概念 (豆電球の並列つなぎの思考実験。パラ数を2個じゃなくて1000個ぐらいで考えれば納得できるだろう)
・LとかCの時間微分がRに見えたりする話
・電力変換 モーターとか。「ちょっと待て、そのR本当にRか?機械エネルギーや化学エネルギーは回生できるぞ。その場合どう表現するか?」
・電池とかフライホイールが何C・Vに相当するか、とか。
・機械負荷等をRで書いたらもうエネルギー変換を意味している
・音響系でも同じような話ができそうだが、普通のスピーカーは非常に効率が悪いので、Misleadingになる。
<システムの中の抵抗>
・整合とSN,NF
・アッテネーター
・実用回路として。減衰器
・Rs,RLも存在した上で値を決める場合、計算が結構めんどくさい
・RC回路、RL回路 (2ポート)
・線形システムを語る 伝達関数、インパルス応答
・実装時の留意点 接地R、入力G
・エネルギー供給・散逸・蓄積の話 ・・消費電力の発生メカニズム (脱線:Sw-CAP抵抗におけるエネルギー運搬)
・干渉1 端子の導体にカップリングするなら単にノイズ重畳
・干渉2 共通インピーダンス
・干渉3 抵抗体そのものにカップリングして、抵抗値の発生する因子を変調 → 能動素子(JFET) .
電熱線
R0 V0 を印加する 電流I0=V0/R0 電力P0=V02/R0 電力を2倍にしたいときどうするか
(1)2パラにする R0→R0/2
電力 P1=V02/(R0/2) = 2V02/R0 = 2P0
このときの電流 I1=V0/(R0/2) = 2V0/R0 =2 I0
電圧x1 電流x2 ⇒ 電力x2
(2)電圧を√2倍にする V0→√2V0
電力 P2=(√2V0)2/R0 = 2V02/R0 = 2P0
このときの電流 I2= √2V0 /R0 = √2I0
電圧x√2 電流x√2 ⇒ 電力x2
(3)2直にして電圧2倍
電力 P3=(2V0)2/2R0 = 2V02/R0 = 2P0
このときの電流 I2= 2V0 /2R0 = I0
電圧x2 電流x1 ⇒ 電力x2
●抵抗にこだわる 2
<抵抗の非理想性>
・遅延 → 電磁気、ポインティングベクトル (脱線:電磁気にも運動量があるそうな。これによって電磁力が偶力として作用する場合にも角運動量保存)
・伝送路、特性インピーダンスは実在する物理量(反射波が戻ってくる前はV/I=Z)
・L、C、寄生成分 等価回路@1ポート
・非線形と歪
・電力消費、発熱(オームの法則からのずれ)、マイグレーション、焼損
・熱雑音 →kTBの証明
<変な抵抗ネットワーク>
演習で出てきそうな変な回路を、目的と合わせて提示して解かせ、パラメータ依存性まで理解させる(既存の教科書は、この最後をやってくれていないのだ)
・ブリッジ(馬鹿正直)~ 同電位短絡
・Rグリッド (接地抵抗の基礎だし、LSIの基板抵抗の取り扱いでも重要)
そしてインピーダンスの概念
●L,C (ハミルトン系としての理解を目指したい)
・そもそもどんな形をしているか(LSI、個別部品)
・なぜ電力消費しないか。まずは、Sin交流の波形を眺めて+/ー相殺のイメージを与えられるが、それだけでは不足。だれかが肩代わりしているはず。
・事実、ステップ電圧印加する時に、蓄積される電力と同じ電力がRで消費される
・蓄積されるエネルギー1/2 LI^2 1/2CV^2 残りの半分はどうなったの? (運動エネルギーでも同じはなしか)
・明示的にRがないときに無限大の電流(電圧)が発生するが、これはどう取り扱うのか
・力学との対応
一般化運動量に対応するものは? Φ ? Q ?
一般化座標に対応するものは? Φ ? Q ?
・力学でいう㎎hはどこに出てくるのか
・インピーダンスの概念
・交流理論は、振動学などで昔からあった。交流電源は発電機・電動機の文脈とともに「発明されたもの」。回転する物体と、sin,cos,exp(i)との対応付けは、だれもが自然に受け入れたのではないか
・交流理論によって、対象の特性も入出力も同じ算数で代数的にハンドリングできるようになっていることが革命的なのである。さらに重ね合わせが成り立つならば百人力。重ね合わせはベクトル解析や
線形空間論においてその意味付けがなされている。
・入力での重ね合わせはいろいろ検討したが、特性の重ね合わせはどうか? (摂動論のようにちょっと変わるってのはある。大きく変わったらどういうことになるか)
V(jw)≒(Zo(jw)+h*Z1(jo)I(jw)
摂動で扱う前に、そもそも単純な足し算の場合をどう表現するか? (Rが1本から2本に増えたような場合)
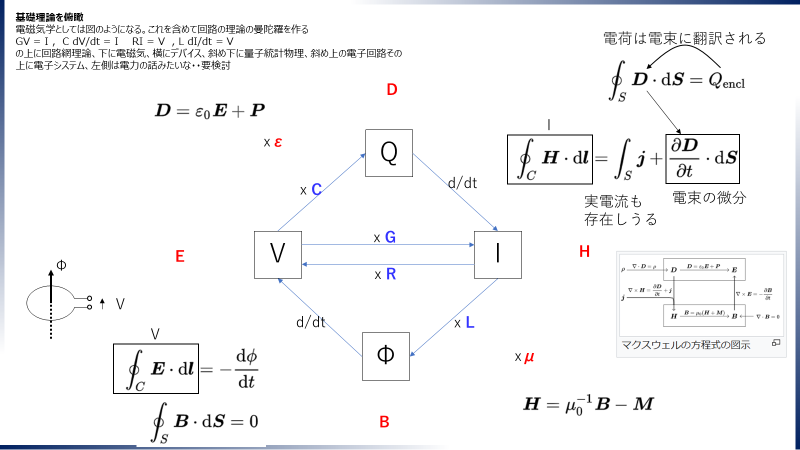
基礎理論を俯瞰